Colors
The semantics of colors is the one ascribed to Gg.color: colors are in a linearized sRGBA space.
Color stops
A value of type Gg.Color.stops specifies a color at each point of the 1D unit space. It is defined by a list of pairs (ti, ci) where ti is a value from 0 to 1 and ci the corresponding color at that value. Colors at points between ti and ti+1 are linearly interpolated between ci and ci+1. If ti lies outside 0 to 1 or if ti-1 >= ti the semantics is undefined.
Given a stops value stops = [(t0, c0); (t1,c1); ... (tn, cn)] and any point t of 1D space, the semantic function:
[] : Gg.Color.stops -> float -> Gg.color
maps them to a color value written [stops]t as follows.
- [
stops]t =(0, 0, 0, 0)for anytifstops = [] - [
stops]t= c0 ift < t0. - [
stops]t= cn ift >= tn. - [
stops]t= (1-u)ci+ uci+1 withu = (t - ti)/(ti+1-ti)ifti<= t <ti+1
Images
Values of type Vg.image represent maps from the infinite 2D euclidian space to colors. Given an image i and a point pt of the plane the semantic function
[]: image -> Gg.p2 -> Gg.color
maps them to a color value written [i]pt representing the image's color at this point.
Paths and areas
A value of type Vg.path is a list of subpaths. A subpath is a list of directed and connected curved segments. Subpaths are disconnected from each other and may (self-)intersect.
A path and an area specification of type Vg.P.area define a finite area of the 2D euclidian space. Given an area specification a, a path p and a point pt, the semantic function:
[]: P.area -> path -> Gg.p2 -> bool
maps them to a boolean value written [a, p]pt that indicates whether pt belongs to the area or not.
The semantics of area rules is as follows:
- [
`Anz,p]ptistrueiff the winding number ofparoundptis non zero. To determine the winding number cast a ray fromptto infinity in any direction (just make sure the ray doesn't intersectptangently or at a singularity). Starting with zero add one for each intersection with a counter-clockwise oriented segment ofpand substract one for each clockwise ones. The resulting sum is the winding number. This is usually refered to as the non-zero winding rule and is the default forVg.I.cut.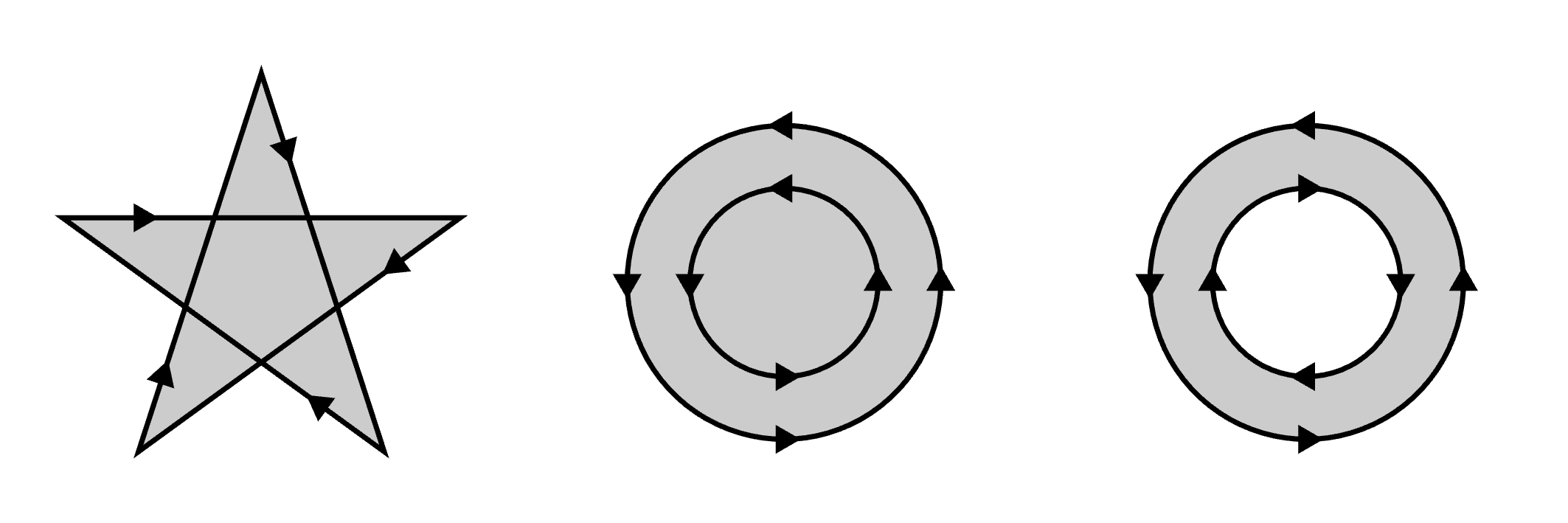
- [
`Aeo,p]ptistrueiff the number of intersections ofpwith a ray cast fromptto infinity in any direction is odd (just make sure the ray doesn't intersectptangently or at a singularity). This is usually refered to as the even-odd rule.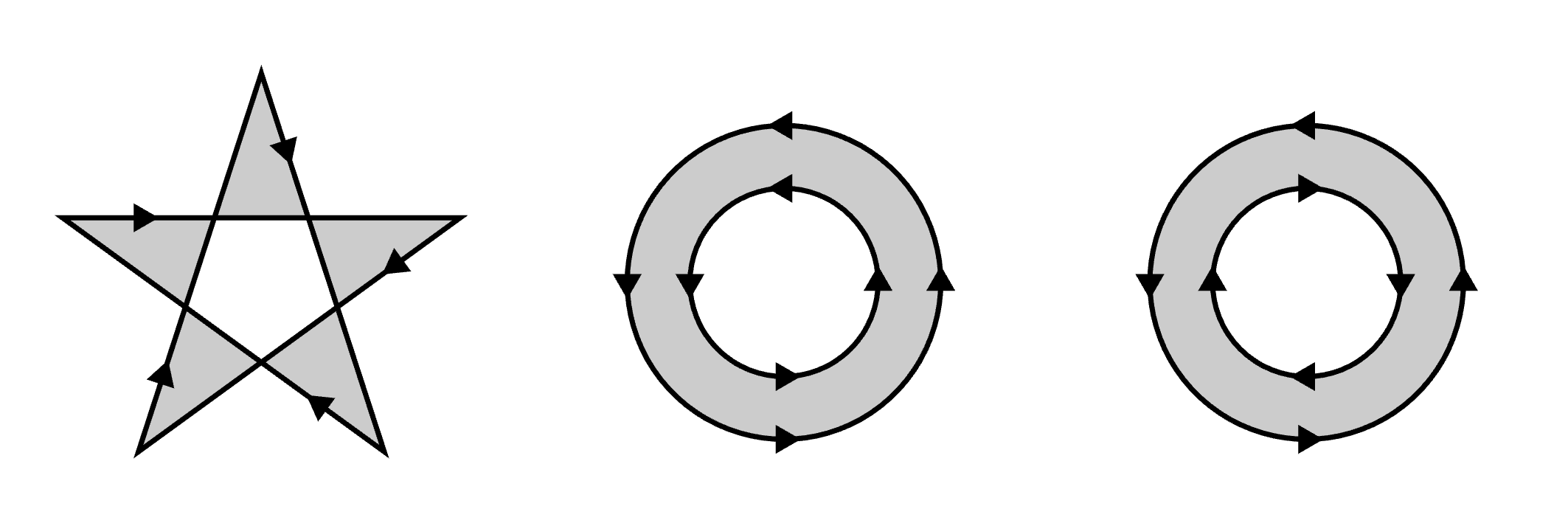
- [
`O o,p]ptistrueiffptis in the outline area ofpas defined by the valueoof typeVg.P.outline. See Outline areas, Segment jointures, Subpath caps, Outline dashes.
Outline areas
The outline area of a path specified by a value o of type Vg.P.outline is the union of its subpaths outline areas.
A subpath outline area is inside the parallel curves at a distance o.width / 2 of its path segments that are joined accoring to the join style o.join (see below) and closed at the subpath end points with a cap style o.cap (see below). The outline area of a subpath can also be chopped at regular intervals according to the o.dashes parameter (see below).
Segment jointures
The shape of subpath segment jointures is specified in o.join by a value of type Vg.P.join. From left to right: 
`Miter, the outer parallel curves are extended until they meet unless the joining angle is smaller thano.miter_anglein which case the join is converted to a bevel.`Round, joins the outer parallel curves by a semicircle centered at the end point with a diameter equal too.width.`Bevel, joins the outer parallel curves by a segment.
Subpath caps
The shape of subpath (or dashes) end points is specified in o.cap by a value of type Vg.P.cap. From left to right: 
`Butt, end points are square and extend only to the exact end point of the path.`Round, end points are rounded by a semicircle at the end point with a diameter equal too.width.`Square, end points are square and extend by a distance equal to halfo.width.
Outline dashes
The path outline area can be chopped at regular intervals by specifying a value (off, pat) of type Vg.P.dashes in o.dashes.
The dash pattern pat is a list of lengths that specify the length of alternating dashes and gaps (starting with dashes). The dash offset off is a positive offset that indicates where to start in the dash pattern at the beginning of a subpath.