The Vg tutorial

Vg is designed to be opened in your module. This defines only types and modules in your scope. Thus to use Vg start with :

open Gg
open Vg

Gg gives us types for points (Gg.p2), vectors (Gg.v2), 2D extents (Gg.size2), rectangles (Gg.box2) and colors (Gg.color).

Later you may want to read Gg's documentation basics but for now it is sufficient to know that each of these types has a literal constructor named v in a module named after the capitalized type name – P2.v, V2.v, etc.

A collage model

Usual vector graphics libraries follow a painter model in which paths are filled, stroked and blended on top of each other to produce a final image. Vg departs from that, it has a collage model in which paths define 2D areas in infinite images that are cut to define new infinite images to be blended on top of each other.

The collage model maps very well to a declarative imaging model. It is also very clear from a specification point of view, both mathematically and metaphorically. This cannot be said from the painter model where the semantics of an operation like stroking a self-intersecting translucent path —  which usually applies the paint only once —  doesn't directly map to the underlying paint stroke metaphor. The collage model is also more economical from a conceptual point view since image cuts and blends naturally unify the distinct concepts of clipping paths, path strokes, path fills and compositing groups (unsupported for now in Vg) of the painter model.

The collage model introduced in the following sections was stolen and adapted from the following works.

Infinite images

Images are immutable and abstract value of type image. Conceptually, images are seen as functions mapping points of the infinite 2D plane to colors:

type Vg.image ≈  Gg.p2 -> Gg.color

The simplest image is a constant image: an image that associates the same color to every point in the plane. For a constant gray of intensity 0.5 this would be expressed by the function:

fun _ -> Color.gray 0.5

In Vg the combinator Vg.I.const produces constant infinite images, the above function is written:

let gray = I.const (Color.gray 0.5)

The module Vg.I contains all the combinators to define and compose infinite images. We will explore some of them later. But for now let's just render that fascinating image.

Rendering

An infinite image alone cannot be rendered. We need a finite view rectangle and a specification of that view's physical size on the render target. These informations are coupled together with an image to form a Vg.Vgr.renderable.

Renderables can be given to a renderer for display via the function Vg.Vgr.render. Renderers are created with Vg.Vgr.create and need a render target value that defines the concrete renderer implementation used (PDF, SVG, HTML canvas etc.).

The following function outputs the unit square of gray on a 30x30 millimeters SVG target in the file /tmp/vg-tutorial.svg:

let svg_of_unit_square i =
  try
    Out_channel.with_open_bin "/tmp/vg-tutorial.svg" @@ fun oc ->
    let size = Size2.v 30. 30. (* mm *) in
    let view = Box2.unit in
    let r = Vgr.create (Vgr_svg.target ()) (`Channel oc) in
    ignore (Vgr.render r (`Image (size, view, i)));
    ignore (Vgr.render r `End);
  with Sys_error e -> prerr_endline e

let () = svg_of_unit_square gray

The result should be an SVG image with a gray square like this:

Coordinate space

Vg's cartesian coordinate space has its origin at the bottom left with the x-axis pointing right, the y-axis pointing up.

It has no units, you define what they mean to you. However a renderable implicitely defines a physical unit for Vg's coordinate space: the corners of the specified view rectangle are mapped on a rectangular area of the given physical size on the target.

Scissors and glue

Constant images can be boring. To make things more interesting Vg gives you scissors: the Vg.I.cut combinator.

This combinator takes a finite area of the plane defined by a path path (more on paths later) and a source image img to define the image I.cut path img that has the color of the source image in the area defined by the path and the invisible transparent black color (Gg.Color.void) everywhere else. In other words I.cut path img represents this function:

fun pt -> if inside path pt then img pt else Color.void

The following code cuts a circle of radius 0.4 centered in the unit square in the gray image defined before.

let circle = P.empty |> P.circle (P2.v 0.5 0.5) 0.4
let gray_circle = I.cut circle gray

Rendered by svg_of_unit_square the result is:

Note that the background color surrounding the circle does not belong to the image itself, it is the color of the webpage background against which the image is composited. Your eyes require a wavelength there and Gg.Color.void cannot provide it.

Vg.I.cut has an optional area argument of type Vg.P.area that determines how a path should be interpreted as an area of the plane. The default value is `Anz, which means that it uses the non-zero winding number rule and for circle that defines its interior.

But the circle path can also be seen as defining a thin outline area around the ideal mathematical circle of circle. This can be specified by using an outline area `O o. The value o of type Vg.P.outline defines various parameters that define the outline area; for example its width. The following code cuts the circle outline area of width 0.04 in an infinite black image.

let circle_outline =
  let area = `O { P.o with P.width = 0.04 } in
  let blue = I.const (Color.v_srgb 0.000 0.439 0.722) in
  I.cut ~area circle blue

Below is the result and again, except for the blue color, the rest is in fact Gg.Color.void.

Vg.I.cut gives us scissors but to combine the results of cuts we need some glue: the Vg.I.blend combinator. This combinator takes two infinite images front and back and defines an image I.blend front back that has the colors of front alpha blended on top of those of back. I.blend front back represents this function:

let i' = fun pt -> Color.blend (front pt) (back pt)

If we blend circle_outline on top of gray_circle:

let dot = I.blend circle_outline gray_circle

We get:

The order of arguments in I.blend is defined so that images can be blended using the left-associative composition operator |>. That is dot can also be written as follows:

let dot = gray_circle |> I.blend circle_outline

This means that with |> and Vg.I.blend left to right order in code maps to back to front image blending.

Transforming images

The combinators Vg.I.move, Vg.I.rot, Vg.I.scale, and Vg.I.tr allow to perform arbitrary affine transformations on an image. For example the image I.move v i is i but translated by the vector v, that is the following function:

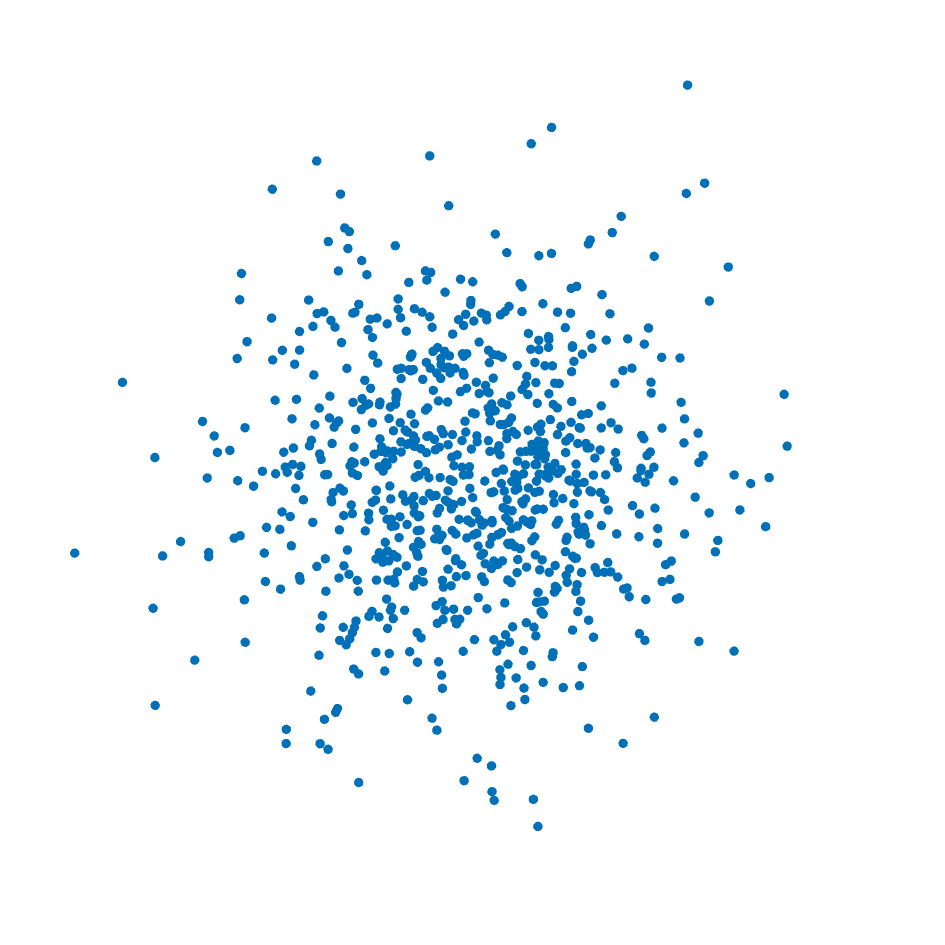
fun pt -> img (V2.(pt - v))

The following example uses Vg.I.move. The function scatter_plot takes a list of points and returns a scatter plot of the points. First we define a dot around the origin, just a black circle of diameter pt_width. Second we define the function mark that given a point returns an image with dot at that point and blend_mark that blends a mark at a point on an image. Finally we blend all the marks together.

let scatter_plot pts pt_width =
  let dot =
    let circle = P.empty |> P.circle P2.o (0.5 *. pt_width) in
    I.const (Color.v_srgb 0.000 0.439 0.722) |> I.cut circle
  in
  let mark pt = dot |> I.move pt in
  let blend_mark acc pt = acc |> I.blend (mark pt) in
  List.fold_left blend_mark I.void pts

Note that dot is defined outside mark, this means that all marks share the same dot, doing so allows renderers to perform space and time optimizations. For example the SVG renderer will output a single circle path shared by all marks.

Here's the result of scatter_point on 800 points with coordinates on independent normal distributions.

Paths

Paths are used to define areas of the plane. A path is an immutable value of type Vg.path which is a list of disconnected subpaths. A subpath is a list of directed and connected curved segments.

To build a path you start with the empty path Vg.P.empty, give it to Vg.P.sub to start a new subpath and give the result to Vg.P.line, Vg.P.qcurve, Vg.P.ccurve, Vg.P.earc or Vg.P.close to add a new segment and so forth.

Path combinators take the path they act upon as the last argument so that the left-associative operator |> can be used to construct paths.

The image below is made by cutting the outline of the single path p defined hereafter.

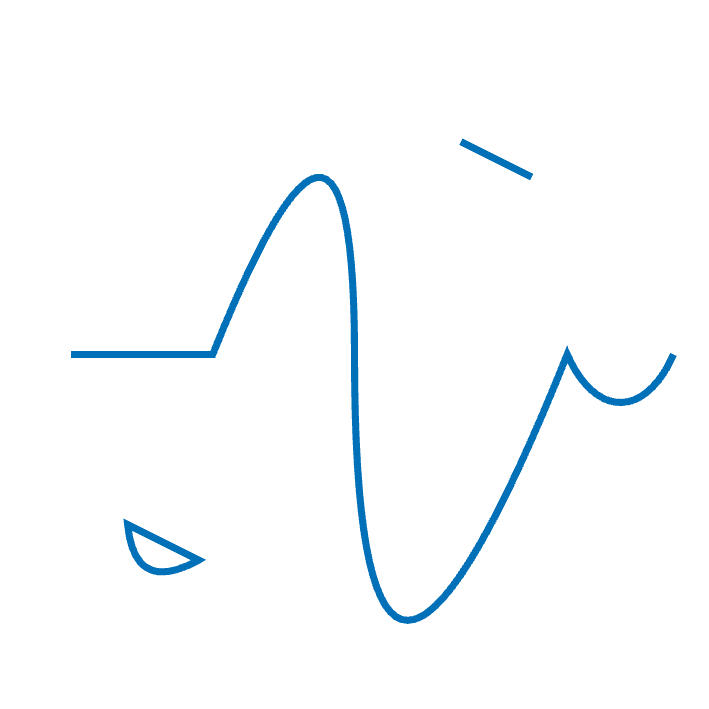
let p =
  let rel = true in
  P.empty |>
  P.sub (P2.v 0.1 0.5) |>
    P.line (P2.v 0.3 0.5) |>
    P.qcurve ~rel (P2.v 0.2 0.5) (P2.v 0.2 0.0) |>
    P.ccurve ~rel (P2.v 0.0 (-. 0.5)) (P2.v 0.1 (-. 0.5)) (P2.v 0.3 0.0) |>
    P.earc ~rel (Size2.v 0.1 0.2) (P2.v 0.15 0.0) |>
  P.sub (P2.v 0.18 0.26) |>
    P.qcurve ~rel (P2.v (0.01) (-0.1)) (P2.v 0.1 (-. 0.05)) |>
    P.close |>
  P.sub (P2.v 0.65 0.8) |>
    P.line ~rel (P2.v 0.1 (-. 0.05))
in
let area = `O { P.o with P.width = 0.01 } in
I.const (Color.v_srgb 0.000 0.439 0.722) |> I.cut ~area p

Except for Vg.P.close which has no other argument but a path, the last point argument before the path argument is always the concrete end point of the segment. When true the optional rel argument indicates that the coordinates given to the constructor are expressed relative to end point of the last segment (or P2.o if there is no such segment).

Note that after a P.close or on the P.empty path, the call to P.sub can be omitted. In that case an implicit P.sub P2.o is introduced.

For more information about how paths are intepreted as areas, consult their semantics.

Remarks and tips